Chapitre 4 Aspect computationnel

Dans cette partie, nous nous intéresserons brièvement à l’aspect computationnel des méthodes qui ont été présentées dans les chapitres précédents. Le développement d’outils logiciels destinés à l’exploration de données génétiques volumineuses requiert qu’une attention particulière soit portée à l’utilisation des ressources de calcul. Étant donné que nous nous intéressons à la possibilité de réaliser des scans génomiques pour des données génétiques de grande taille, il semblait intéressant de préciser les points sur lesquels des améliorations ont été faites d’un point de vue computationnel.

4.1 Du langage C au langage R

La première version de pcadapt a été implémentée par Nicolas Duforet-Frebourg. Le logiciel a été initialement développé en C mais nous avons décidé de poursuivre le développement du logiciel en R/Rcpp, afin de simplifier son utilisation et de bénéficier des performances du langage C++, mais surtout de la portabilité, des outils de visualisation et de documentation du langage R. La librairie pcadapt est disponible sur CRAN.

4.2 Du calcul de la matrice de covariance à l’algorithme IRAM

Nous rappelons ici que nous nous intéressons seulement aux premières composantes principales obtenues avec l’ACP, ce qui signifie qu’il n’est pas nécessaire d’effectuer la décomposition en valeurs singulières (SVD) complète de la matrice d’apparentement génétique \(G_{RM} \in \mathcal{M}_{n}(\mathbb{R})\) (où \(n\) est le nombre d’individus). Il s’agit de ce que l’on appelle une décomposition en valeurs singulières tronquée. Pour effectuer l’ACP à partir d’une matrice de génotypes \(\tilde{G} \in \mathcal{M}_{np}(\mathbb{R})\), il est donc nécessaire de calculer la matrice d’apparentement génétique \(G_{RM}\) pour ensuite calculer la SVD de \(G_{RM}\). En suivant cette procédure, le calcul de la matrice \(G_{RM}\) est l’étape la plus coûteuse d’un point de vue algorithmique, car de complexité quadratique en le nombre d’individus. Cependant de nouvelles méthodes permettent d’effectuer la SVD tronquée de \(G_{RM}\) sans qu’il n’y ait besoin de calculer explicitement \(G_{RM}\). La méthode que nous avons choisie d’utiliser pour le calcul de l’ACP est basée sur l’algorithme IRAM (Implicitly Restarted Arnoldi Method) (Calvetti, Reichel, & Sorensen, 1994; Lehoucq & Sorensen, 1996).

L’algorithme IRAM repose sur l’idée que les vecteurs propres d’une matrice carrée \(A \in \mathcal{M}_{n}(\mathbb{R})\) peuvent être estimés en construisant une base orthogonale de l’espace vectoriel \(\mathcal{K}_k(x) = \text{Vect}(x, Ax, A^2x, \dots, A^kx)\) engendré par les itérations de \(A\) où \(x \in \mathbb{R}^n\) et \(k \in \mathbb{N}\). \(\mathcal{K}_k(x)\) est connu sous le nom d’espace de Krylov. Dans notre cas, la matrice carrée que l’on souhaite décomposer est la matrice \(G_{RM}\). Pour construire les espaces de Krylov associés à \(G_{RM}\), il faut donc calculer les produits \(G_{RM}x\). Or, pour ne pas avoir à calculer \(G_{RM}\) lors du calcul de \(G_{RM}x\) (nous rappelons que \(G_{RM} = \frac{1}{p}\tilde{G}\tilde{G}^T\)), il suffit de calculer d’abord \(y = \frac{1}{\sqrt{p}}\tilde{G}^Tx\) puis \(\frac{1}{\sqrt{p}}\tilde{G}y\), résultant en un coût algorithmique linéaire en \(n\) et en \(p\) (Figure 4.1).

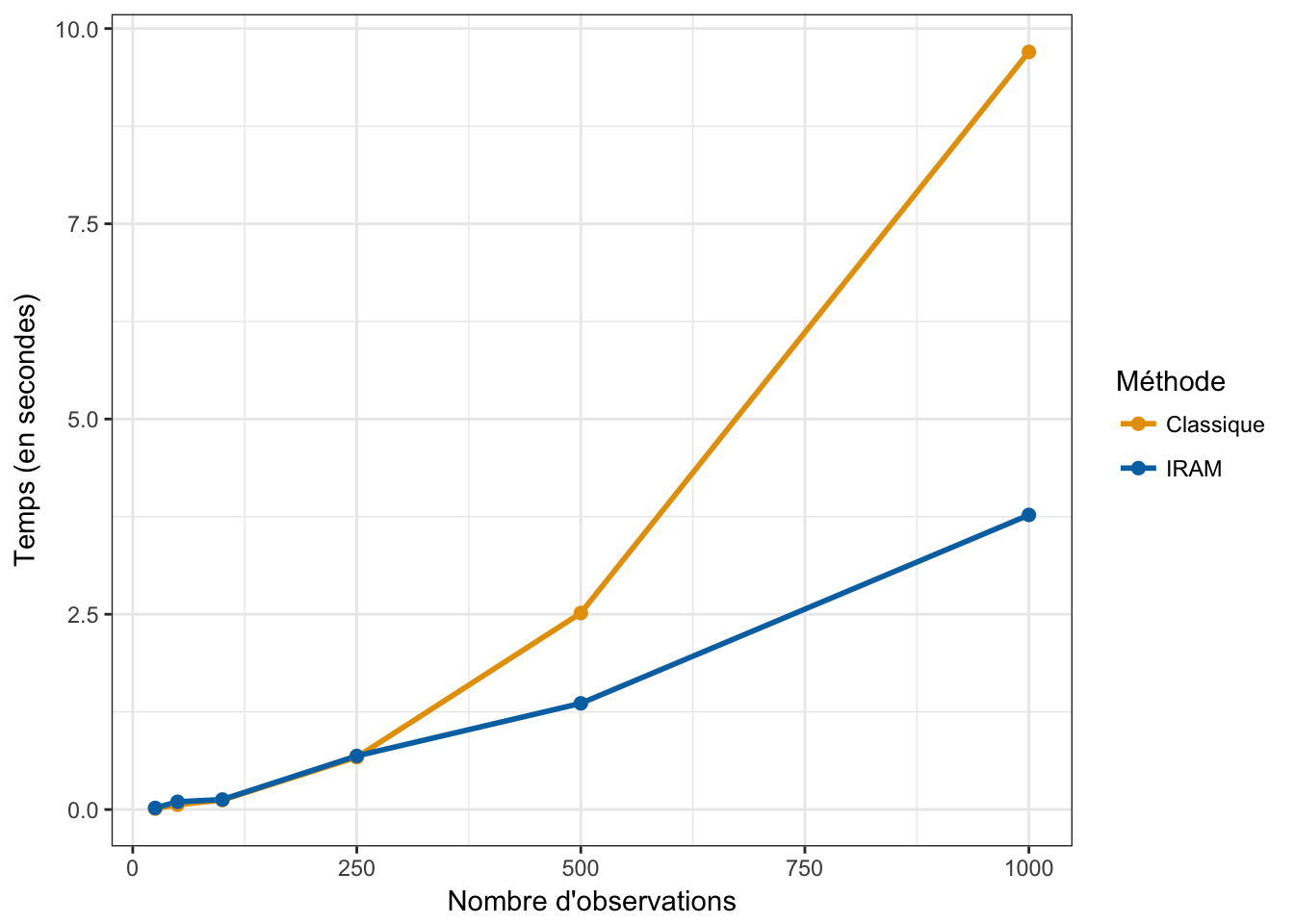
Comparaison des temps de calcul pour la SVD tronquée de rang 2 obtenue avec la méthode classique et la méthode IRAM. Le nombre de variables est fixé à 10000 et le nombre d’observations varie de 25 à 1000. Nous constatons que pour un nombre d’observations élevé, l’algorithme IRAM est plus efficace que la méthode nécessitant de calculer la matrice de covariance.

Figure 4.1: Comparaison des temps de calcul pour la SVD tronquée de rang 2 obtenue avec la méthode classique et la méthode IRAM. Le nombre de variables est fixé à 10000 et le nombre d’observations varie de 25 à 1000. Nous constatons que pour un nombre d’observations élevé, l’algorithme IRAM est plus efficace que la méthode nécessitant de calculer la matrice de covariance.

4.3 ACP et valeurs manquantes

Pour tenir compte de la présence de données manquantes dans le calcul de l’ACP, plusieurs stratégies peuvent être envisagées (Dray & Josse, 2015) :

  • Imputer : chaque entrée manquante est remplacée par une valeur et l’ACP est réalisée à partir de la matrice de génotypes complétée. Dans le logiciel flashpca par exemple, si la valeur \(G_{ij}\) est manquante, elle complétée par la valeur moyenne observée sur le \(j\)-ème locus (Abraham & Inouye, 2014). D’autres suggèrent encore d’utiliser des logiciels spécifiquement conçus pour l’imputation de données génétiques comme Beagle ou SHAPEIT (Browning & Browning, 2016; Delaneau, Marchini, & Zagury, 2012).

  • Tenir compte des données manquantes dans le calcul de \(G_{RM}\) : lors du calcul de la corrélation entre deux individus \(i\) et \(j\), sont exclus du calcul tout marqueur génétique manquant chez l’individu \(i\) ou \(j\).

\[\begin{equation} G_{RM, ij} = \frac{1}{\sum_{k=1}^p \delta_{ik}\delta_{jk}} \sum_{k = 1}^p \frac{(G_{ik} - 2p_k) \times (G_{jk} - 2p_k)}{2p_k(1-p_k)} \delta_{ik} \delta_{jk} \tag{4.1} \end{equation}\]

où \(\delta_{ik} = 0\) si \(G_{ik}\) est manquant et \(\delta_{ik} = 1\) sinon. Dans le cas où il n’y a pas de valeur manquante, nous retrouvons bien l’expression donnée par l’équation (2.5). Un exemple d’implémentation en Rcpp du calcul de \(G_{RM}\) tenant compte des données manquantes est donné ci-dessous.

#include <Rcpp.h>
using namespace Rcpp;

// [[Rcpp::export]]
NumericMatrix PairGRM(const NumericMatrix &G,
                      const NumericVector &p) {

  // In our algorithms, individuals are stored in columns 
  // and SNPs are stored in rows.
   
  int nSNP = G.nrow(); // number of SNPs
  int nIND = G.ncol(); // number of individuals
  NumericMatrix GRM(nIND, nIND); // Genetic Relationship Matrix

  for (int i = 0; i < nIND; i++) {
    for (int j = 0; j < nIND; j++) {

      // value = GRM(i, j)
      double value = 0;
      double tmp = 0; 
      // number of missing values for each pair 
      // of individuals (i, j)
      // nbmv = \sum_{k = 1}^{nSNP} \delta_{ik} \delta{jk}
      int nbmv = 0;

      // Loop over the SNPs to compute the dot product
      for (int k = 0; k < nSNP; k++) {
        if ((!NumericVector::is_na(G(k, i))) && 
            (!NumericVector::is_na(G(k, j)))) {
          tmp = (G(k, i) - 2 * p[k]) * (G(k, j) - 2 * p[k]);
          value +=  tmp / (2 * p[k] * (1 - p[k]));
        } else {
          nbmv++;
        }
      }
      // Divide by the number of non-missing values for (i, j)
      GRM(i, j) = value / (nSNP - nbmv);
    }
  }
  return GRM;
}

Algorithme IRAM et données manquantes

Cependant, comme cela a été dit dans le paragraphe précédent, nous souhaitons nous détacher du calcul de la matrice \(G_{RM}\). Nous avons donc cherché à adapter l’algorithme IRAM pour qu’il puisse tenir compte de la présence de données manquantes, à la manière de la fonction PairGRM décrite ci-dessus. Nous avons donc adopté la même démarche, mais en l’appliquant aux produits \(\tilde{G}^Tx\) et \(\tilde{G}y\) où \(x \in \mathbb{R}^n\) et \(y \in \mathbb{R}^p\). Plus précisément, plutôt que de calculer \(\tilde{G}^Tx\) et \(\tilde{G}y\), nous calculons les produits \(\frac{1}{n}\tilde{G}^Tx\) et \(\frac{1}{p}\tilde{G}y\), ce qui nous permet de tenir compte des données manquantes de la façon suivante :

\[\begin{equation} \begin{split} \forall j \in [|1,p|], \; \left(\frac{1}{n}\tilde{G}^Tx\right)_j &= \frac{1}{\sum_{i=1}^n \delta_{ij}} \sum_{i = 1}^n \tilde{G}_{ij} \delta_{ij} x_i, \\ \forall i \in [|1,n|], \; \left(\frac{1}{p}\tilde{G}y\right)_i &= \frac{1}{\sum_{j=1}^p \delta_{ij}} \sum_{j = 1}^p \tilde{G}_{ij} \delta_{ij} y_j, \end{split} \tag{4.2} \end{equation}\]

où \(\delta_{ij} = 0\) si \(G_{ij}\) est manquant et \(\delta_{ij} = 1\) sinon. En l’absence de données manquantes, cette méthode donne une estimation du produit \(\frac{1}{np}\tilde{G}\tilde{G}^Tx = \frac{1}{n}G_{RM}x\), ce qui signifie que si l’on applique l’algorithme IRAM en utilisant les produits définis à l’équation (4.2), nous obtenons la SVD de \(\frac{1}{n}G_{RM}\) et non pas celle de \(G_{RM}\). Pour déduire la SVD de \(G_{RM}\) à partir de la SVD de \(\frac{1}{n}G_{RM}\), il suffit simplement de multiplier les valeurs propres de \(\frac{1}{n}G_{RM}\) par \(n\), les vecteurs propres étant les mêmes pour les deux décompositions.

Précision de la SVD en présence de données manquantes

Nous comparons ici les différentes méthodes dont nous avons parlé dans le paragraphe précédent, à savoir flashpca, PairGRM et notre nouvelle méthode. La comparaison est réalisée sur un échantillon du jeu de données POPRES. Nous évaluons la sensibilité des différentes méthodes à la présence de données manquantes en comparant les valeurs singulières et les scores de l’ACP obtenus par chacune des méthodes en présence de données manquantes aux valeurs singulières et scores de l’ACP obtenus avec flashpca en l’absence de données manquantes. Les résultats de cette comparaison sont donnés en figure 4.2.

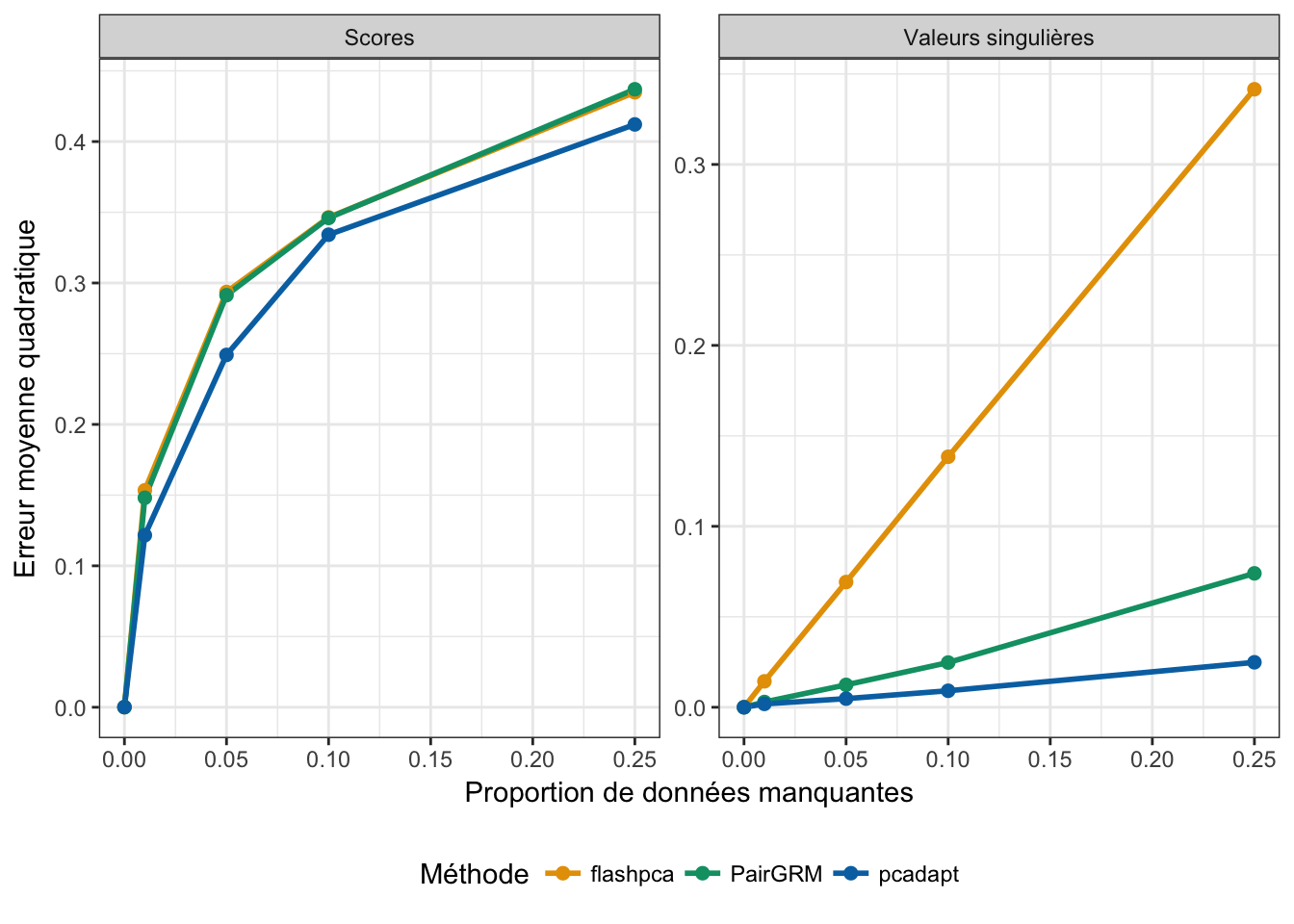
Comparaison des scores d’ACP obtenus avec flashpca, PairGRM et pcadapt pour différentes proportions de valeurs manquantes distribuées uniformément. Nous calculons l’erreur moyenne quadratique pour le calcul des 5 premiers axes de l’ACP et des 5 premières valeurs singulières.

Figure 4.2: Comparaison des scores d’ACP obtenus avec flashpca, PairGRM et pcadapt pour différentes proportions de valeurs manquantes distribuées uniformément. Nous calculons l’erreur moyenne quadratique pour le calcul des 5 premiers axes de l’ACP et des 5 premières valeurs singulières.

En conclusion, la possibilité de déduire la SVD d’une matrice \(A\) à partir de la SVD d’une matrice proportionnelle à celle-ci nous a permis d’adapter la méthode IRAM au cas de matrices contenant des données manquantes. Par ailleurs, d’après nos comparaisons numériques, notre nouvelle méthode s’avère être moins sensible à la présence de données manquantes.

4.4 Du format .pcadapt au format .bed

Le format .pcadapt stocke la matrice de génotypes dans un fichier texte où chaque ligne représente un marqueur génétique. Les caractères sont séparés par un espace et les valeurs manquantes sont encodées par des 9. Ce format a été utilisé car le calcul de l’ACP pouvait être effectué sans qu’il n’y ait besoin de charger la matrice de génotypes dans la mémoire vive. La matrice \(G_{RM}\) était alors calculée de façon incrémentale, en parcourant le fichier ligne par ligne (et donc SNP par SNP). Ce format, bien que très simple, présente quelques inconvénients :

  • les espaces n’encodent aucune information. La moitié de l’espace mémoire occupée par le fichier est donc essentiellement vide d’un point de vue informatif.

  • les génotypes 0, 1, 2 et 9 sont encodés en ASCII et donc chaque valeur occupe un octet (ou 8 bits).

Le logiciel PLINK (Purcell et al., 2007) dispose quant à lui du format de fichier .bed qui semble plus adapté au développement logiciel :

  • le format .bed est un format de fichier binaire, l’accès à un fichier binaire est plus rapide que l’accès à un fichier texte.

  • sachant qu’il n’y a que 4 valeurs possibles pour un génotype, chaque génotype peut être encodé sur 2 bits (Table 4.1).

Table 4.1: Encodage des génotypes dans le format .bed. Les génotypes sont encodés sur 2 bits ce qui permet de stocker 4 génotypes sur un octet, contrairement au format .pcadapt où chaque génotype est encodé sur un octet. Le quadruplet 2 1 NA 2 sera par exemple encodé par 11100111.
Génotype Encodage
0 00
NA 01
1 10
2 11

Pour résumer, un fichier .bed et un fichier .pcadapt contiennent exactement la même information. Un fichier .bed occupe exactement 8 fois moins d’espace mémoire physique qu’un fichier au format .pcadapt. Nous avons donc décidé de développer nos algorithmes afin qu’ils puissent être directement utilisés sur des fichiers .bed sans qu’il n’y ait besoin de les convertir au format .pcadapt.

4.5 Interface Shiny

Nous proposons également une interface graphique, basée sur la librairie Shiny, pour une utilisation simplifiée de nos outils statistiques. Cette interface se présente sous la forme d’une application web, et nécessite donc l’utilisation d’un navigateur.

References

Calvetti, D., Reichel, L., & Sorensen, D. C. (1994). An implicitly restarted lanczos method for large symmetric eigenvalue problems. Electronic Transactions on Numerical Analysis, 2(1), 21.

Lehoucq, R. B., & Sorensen, D. C. (1996). Deflation techniques for an implicitly restarted arnoldi iteration. SIAM Journal on Matrix Analysis and Applications, 17(4), 789–821.

Dray, S., & Josse, J. (2015). Principal component analysis with missing values: A comparative survey of methods. Plant Ecology, 216(5), 657–667.

Abraham, G., & Inouye, M. (2014). Fast principal component analysis of large-scale genome-wide data. PloS One, 9(4), e93766.

Browning, B. L., & Browning, S. R. (2016). Genotype imputation with millions of reference samples. The American Journal of Human Genetics, 98(1), 116–126.

Delaneau, O., Marchini, J., & Zagury, J.-F. (2012). A linear complexity phasing method for thousands of genomes. Nature Methods, 9(2), 179–181.