Chapitre 5 Perspectives et conclusions

Nous discutons dans ce chapitre des extensions ou alternatives possibles à ce qui a été présenté jusqu’ici.

5.1 Substitution de l’Analyse en Composantes Principales

La méthode de scan à sélection basée sur la distance de Mahalanobis peut être vue comme la succession de trois étapes :

• une première étape visant à déterminer la structure de populations à partir de l’ACP.

• une deuxième étape consistant à effectuer la régression linéaire multiple de la matrice de génotypes normalisée par les scores de l’ACP.

• une troisième étape calculant la distance de chaque marqueur génétique à la moyenne de ces marqueurs pour une métrique donnée, ce qui permet d’identifier les marqueurs génétiques dont les coefficients de régression sont excessivement corrélés avec une ou plusieurs composantes principales. Dans le cas de la distance de Mahalanobis, la métrique est donnée par l’estimateur robuste de la matrice de covariance.

En réalité, on retrouve ce schéma également pour le calcul de la \(F_{ST}\) :

• structure de populations définie par la matrice de scores \(U_{\delta}\) telle qu’elle est définie dans le chapitre 1.

• régression linéaire multiple de la matrice de \(\tilde{G}\) par les scores \(U_{\delta}\).

• calcul de la distance euclidienne \(||\tilde{G}^TU_{\delta}||_2\) de chaque marqueur à la moyenne des marqueurs (ici la métrique est la matrice identité et la moyenne des marqueurs est la fréquence).

De la même façon, le calcul de la statistique \(T_{F-LK}\) peut être décomposé suivant le schéma décrit ci-dessus. Ces trois étapes communes permettent donc de définir un schéma général pour le développement de nouvelles méthodes de scan génomique. La première étape pourrait très bien être remplacée par des variantes de l’ACP telles qu’une ACP régularisée, une ACP à noyau ou une ACP pondérée.

5.2 Utilisation du déséquilibre de liaison pour améliorer l’inférence de la structure

Lorsque deux marqueurs génétiques sont physiquement proches l’un de l’autre, il y a de fortes chances qu’ils soient corrélés entre eux. Ce phénomène est connu sous le nom de déséquilibre de liaison. Lors de l’inférence de la structure de populations à l’aide de l’ACP, il est généralement recommandé de filtrer ce déséquilibre de liaison en effectuant une procédure de pruning (Abdellaoui et al., 2013; Prive, Aschard, & Blum, 2017). À l’inverse, D. J. Lawson, Hellenthal, Myers, & Falush (2012) suggèrent quant à eux d’inclure cette information et montrent qu’en utilisant leur logiciel fineSTRUCTURE sur des jeux de données relativement denses, la structure de populations est bien mieux estimée qu’avec l’ACP telle qu’elle est implémentée dans EIGENSTRAT (Price et al., 2006). L’utilisation de fineSTRUCTURE ou de méthodes qui prennent en compte le déséquilibre de liaison pour inférer la structure de populations peut donc s’avérer intéressante pour deux raisons. Cela permettrait de ne pas avoir à prétraiter les données pour le déséquilibre de liaison puisqu’il est directement pris en compte. Et surtout, nous nous attendons à ce qu’une meilleure estimation de la structure de population améliore la puissance des test statistiques et réduise le nombre de fausses découvertes. En pratique, pour définir un scan à sélection prenant en compte le déséquilibre de liaison pour l’estimation de la structure, il suffit d’utiliser les scores de l’ACP obtenus avec fineSTRUCTURE à la première étape.

5.3 Utilisation de variables environnementales

Une autre alternative possible serait la prise en compte de variables environnementales pour la détection d’adaptation locale. Notre méthode actuelle suppose que les locus sous adaptation locale devraient être excessivement corrélés avec la structure de populations, qui est représentée par les composantes principales. Dans le cas où la sélection n’est pas liée à la structure de populations, notre méthode n’est plus adaptée. Pour illustrer cela, il suffit de considérer une simulation où les locus sous sélection ne sont pas du tout corrélés à la structure de populations, mais à des variables environnementales qui ne sont pas non plus corrélés à la structure de populations. Nous observons sur la figure 5.1 que notre méthode ne détecte aucun des locus sous adaptation locale. Pour détecter des signaux de ce type, une approche consiste à décorréler les variables environnementales à l’aide d’une analyse des redondances (RDA) (Lasky et al., 2012). Cette analyse produit des nouveaux scores qui sont des combinaisons linéaires des variables environnementales et qui peuvent être utilisées en lieu et places des scores de l’ACP réalisée sur les génotypes. Cette étape est suivie des étapes 2 (régression linéaire multiple) et 3 (distance robuste de Mahalanobis) décrites ci-dessus. Cette procédure fait l’objet d’un travail de recherche de Thibaut Capblancq, post-doctorant au Laboratoire d’Ecologie Alpine à Grenoble.

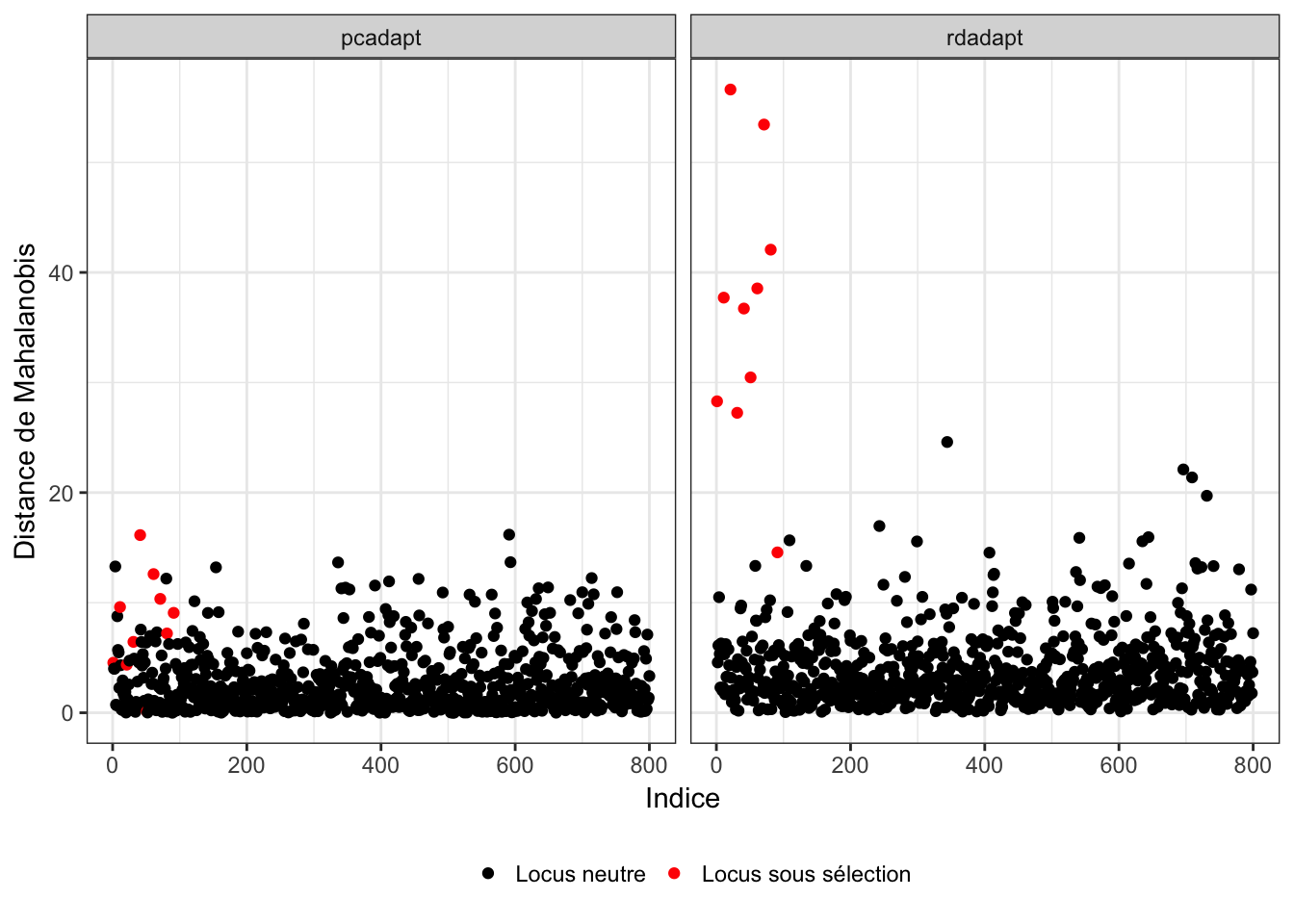
Figure 5.1: Exemple de scan à sélection réalisé avec pcadapt sur une simulation réalisée par Éric Bazin contenant des locus sous sélection qui ne sont pas corrélés à la structure de la population. Les points rouges correspondent aux locus sous sélection pour la simulation.

5.4 Scans pour l’introgression et données manquantes

Dans notre étude portant sur l’introgression, nous n’avons utilisé que des jeux de données complets, puisqu’ils ont été soit simulés, soit imputés à l’aide de Beagle (S. R. Browning & Browning, 2007). Le recours à des logiciels d’imputation est souvent nécessaire car la plupart des méthodes développées ne sont pas utilisables en présence de valeurs manquantes, ce qui est le cas pour notre méthode de scan d’introgression. Il convient toutefois de rappeler que les logiciels d’imputation doivent être utilisés avec précaution, l’imputation de valeurs manquantes très localisées peut créer des motifs particuliers localement sur le génôme susceptibles d’être détectés par les différentes méthodes présentées (Figure 5.2). Une possibilité intéressante serait d’associer aux valeurs manquantes les degrés de confiance avec lesquels celles-ci ont été complétées, ce qui pourrait par exemple permettre de pondérer les statistiques de détection par ces degrés de confiance.

Figure 5.2: Exemple de scans d’introgression à partir de données imputées avec Beagle (S. R. Browning & Browning, 2007) sans prétraitement des données. Les régions uniquement détectées par pcadapt et RFMix (Maples et al., 2013) sont des régions qui en réalité présentent une très grande proportion de valeurs manquantes. Cette figure illustre l’importance de filtrer les marqueurs ayant une proportion trop élevée de valeurs manquantes.

5.5 L’approche IRAM pour les données manquantes

Dans le chapitre précédent, nous avons proposé un moyen d’adapter tout algorithme dérivé de la méthode des puissances itérées à des jeux de données contenant des données manquantes. Notre souhait était de disposer d’une méthode d’ACP de complexité linéaire en \(n\) et \(p\) tout en étant capable d’estimer raisonnablement bien les éléments propres de la matrice d’apparentement génétique, même en présence de données manquantes. La plupart des méthodes d’ACP utilisables sur des jeux de données incomplets affichent souvent des complexités en \(O(\min(n^2p, np^2))\) (Severson, Molaro, & Braatz, 2017), ce que l’on préfère éviter. Notre méthode a été comparée à deux approches. La première est celle utilisée par le logiciel flashpca (Abraham et al., 2017), qui consiste à remplacer les valeurs manquantes par les valeurs moyennes de chaque SNP. La seconde est celle qui était implémentée dans les premières versions de pcadapt. Cette méthode tient compte de la présence de valeurs manquantes dans le calcul de la matrice d’apparentement génétique. Les résultats de notre comparaison, bien que très spécifique (distribution de valeurs manquantes uniforme, données présentant beaucoup de structure), nous confortent dans l’idée de pouvoir intégrer la prise en compte des données manquantes dans des méthodes telles que IRAM, sans pour autant modifier la complexité de l’algorithme. Nous pensons que cette méthode peut toutefois s’avérer efficace pour d’autres types de données ou d’autres types de distributions de valeurs manquantes.

5.6 Conclusion

Alors que le développement technologique des ressources de calcul semble s’essouffler, du fait de la difficulté croissante liée à la miniaturisation des composants électroniques, les données ne cessent quant à elles de s’accumuler, et ce, quelque soit le domaine d’activité. Cette tendance suggère l’utilisation d’algorithmes à faible complexité pour le traitement et l’analyse de ces données. L’Analyse en Composantes Principales se révèle donc être un outil de premier choix pour traiter ces nouveaux volumes de données. En génétique des populations, elle présente l’avantage supplémentaire de très bien s’interpréter par l’intermédiaire de la structure de populations. Pour ces raisons, nous avons développé au cours de cette thèse des méthodes statistiques reposant exclusivement sur l’Analyse en Composantes Principales.

Nous avons tout d’abord montré comment l’utilisation de l’ACP permettait d’étendre les tests classiques de différenciation au cas de populations continues. D’abord parce que l’indice de fixation correspond à la proportion de variance expliquée par un modèle à facteurs discrets, alors que la statistique de communalité renvoie à un modèle à facteurs qui peuvent être discrets ou continus. Ensuite parce que, de même que notre nouvelle statistique, la statistique \(T_{F-LK}\) correspond essentiellement à une distance de Mahalanobis dans le cas de populations discrètes. La principale différence entre ces méthodes réside dans la façon dont sont estimés les moments d’ordre 1 et 2 dans le calcul de la distance de Mahalanobis.

Nous avons ensuite développé une nouvelle approche statistique pour la détection de régions introgressées, basée sur l’utilisation de scores de métissage locaux calculés à partir de l’ACP. Les avantages de cette méthode, par rapport à celles qui sont présentées, sont essentiellement pratiques. La détection de l’introgression via l’estimation des coefficients de métissage locaux requiert souvent l’utilisation conjointe d’une méthode de phasage ou bien la connaissance de certains paramètres biologiques qui ne sont pas forcément bien définis (comme le taux de recombinaison moyen par exemple). De plus, notre méthode est de complexité linéaire par rapport au nombre d’individus ainsi que par rapport au nombre de SNPs, ce qui la rend très rapide à utiliser même pour des jeux de données qui sont amenés à être de plus en plus denses.

Nous avons développé nos méthodes en veillant à proposer un outil simple d’utilisation tout en cherchant à optimiser l’utilisation des ressources de calcul. Malgré ces précautions, il est certain que la librairie pcadapt pourra encore bénéficier d’améliorations, à la fois en termes de méthodologie statistique et en termes d’implémentation. Bien que notre librairie soit destinée à l’analyse de données volumineuses, elle reste à ce jour principalement utilisée sur des matrices de génotypes relativement petites (de l’ordre du million de SNPs et du millier d’individus).

References

Abdellaoui, A., Hottenga, J.-J., De Knijff, P., Nivard, M. G., Xiao, X., Scheet, P., … others. (2013). Population structure, migration, and diversifying selection in the netherlands. European Journal of Human Genetics, 21(11), 1277–1285.

Prive, F., Aschard, H., & Blum, M. G. (2017). Efficient management and analysis of large-scale genome-wide data with two r packages: Bigstatsr and bigsnpr. bioRxiv, 190926.

Lawson, D. J., Hellenthal, G., Myers, S., & Falush, D. (2012). Inference of population structure using dense haplotype data. PLoS Genetics, 8(1), e1002453.

Price, A. L., Patterson, N. J., Plenge, R. M., Weinblatt, M. E., Shadick, N. A., & Reich, D. (2006). Principal components analysis corrects for stratification in genome-wide association studies. Nature Genetics, 38(8), 904.

Lasky, J. R., Des Marais, D. L., McKAY, J., Richards, J. H., Juenger, T. E., & Keitt, T. H. (2012). Characterizing genomic variation of arabidopsis thaliana: The roles of geography and climate. Molecular Ecology, 21(22), 5512–5529.

Browning, S. R., & Browning, B. L. (2007). Rapid and accurate haplotype phasing and missing-data inference for whole-genome association studies by use of localized haplotype clustering. The American Journal of Human Genetics, 81(5), 1084–1097.

Maples, B. K., Gravel, S., Kenny, E. E., & Bustamante, C. D. (2013). RFMix: A discriminative modeling approach for rapid and robust local-ancestry inference. The American Journal of Human Genetics, 93(2), 278–288.

Severson, K. A., Molaro, M. C., & Braatz, R. D. (2017). Principal component analysis of process datasets with missing values. Processes, 5(3), 38.

Abraham, G., Qiu, Y., & Inouye, M. (2017). FlashPCA2: Principal component analysis of biobank-scale genotype datasets. Bioinformatics.