Chapitre 3 Introgression adaptative

Dans la partie précédente nous nous sommes intéressés à la détection d’allèles ayant favorisé l’adaptation d’une population à son environnement. Cependant, les scans génomiques pour la sélection ne permettent pas de comprendre l’origine du mécanisme adaptatif associé. Nous avons vu en introduction que la diversité allélique jouait un rôle important dans les processus d’adaptation locale, en offrant aux populations la possibilité de puiser dans un catalogue d’allèles plus vaste et d’augmenter ainsi leur potentiel adaptatif. Pour cette raison, l’introgression est désormais considérée comme un mécanisme d’adaptation important (Hedrick, 2013). Nous rappelons que l’introgression adaptative correspond à la sélection d’allèles transmis par flux de gènes ou par hybridation, ce qui permet de distinguer deux scénarios évolutifs distincts que nous décrivons ici.

Le premier est un scénario de métissage où deux populations apparentées s’hybrident en donnant naissance à une nouvelle population, si bien que certains allèles provenant d’une des populations parentales peuvent être sélectionnés pour l’environnement dans lequel évolue la population métissée (Figure 3.1).

Le second scénario suppose l’entrée en contact d’une population dite donneuse avec une population dite receveuse, permettant à la population receveuse d’intégrer de nouveaux allèles (Figure 3.1).

Figure 3.1: Scénarios d’introgression. À gauche une représentation schématique du modèle de métissage. À droite une représentation schématique du modèle à flux de gènes. Dans les deux cas, la population jaune correspond à la population ayant bénéfié de gènes par introgression de la part de la population bleue.

Nous présentons dans ce chapitre différents outils statistiques (Table 3.1) pour la détection de signaux d’introgression pour chacun des deux scénarios (Figure 3.1), ainsi qu’une nouvelle approche basée sur l’Analyse en Composantes Principales valable pour les deux types de scénarios.

Table 3.1: Liste des méthodes et des logiciels présentés dans ce chapitre.

Méthode	Scénario	Référence
Loter	Métissage	Dias-Alves et al. (\(in\) \(prep\))
HAPMIX	Métissage	Price et al. (2009)
RFMix	Métissage	Maples et al. (2013)
EILA	Métissage	Yang et al. (2013)
\(D\)	Flux de gènes	Durand et al. (2011)
Bd\(_{f}\)	Flux de gènes	Pfeifer et al. (2017)
\(f_d\)	Flux de gènes	Martin et al. (2014)
\(RND_{min}\)	Flux de gènes	Rosenzweig et al. (2016)

3.1 Introgression par métissage

Nous nous intéressons ici à la détection de signaux d’introgression dans une population métissée, à partir de la donnée de coefficients de métissage locaux. Nous avons vu dans le paragrahe 2.2.3 qu’il était possible d’estimer pour un individu, la proportion de son génôme provenant d’un ou de plusieurs groupes génétiques. Ces proportions sont connues plus communément sous le nom de coefficients de métissage et peuvent servir à mieux comprendre l’histoire démographique des populations métisséees. De nombreux logiciels existent pour l’estimation de ces coefficients : STRUCTURE, ADMIXTURE (Alexander, Novembre, & Lange, 2009), LEA (Frichot & François, 2015), tess3r (Caye, Deist, Martins, Michel, & François, 2016). Chaque individu peut de ce fait être vu comme une mosaïque d’allèles qui ont été puisés dans des groupes génétiques distincts. En revanche, les coefficients de métissage ne renseignent pas sur les portions du génôme qui proviennent effectivement de ces groupes génétiques.

3.1.1 Coefficients de métissage locaux

Chercher à attribuer à chaque allèle la population ancestrale de laquelle il est originaire constitue la problématique d’estimation des coefficients de métissage locaux (Figure 3.2). Avoir à disposition une telle information individuelle et locale permet de quantifier à l’échelle de la population la probabilité qu’un allèle ait été fourni par une population spécifique. Ce type de méthodologie, basé sur l’estimation de coefficients de métissage locaux, a par exemple été employé pour la détection d’introgression adaptative chez les peupliers d’Amérique du Nord (Suarez-Gonzalez, 2016). Encore une fois, plusieurs logiciels ont été proposés dans le but d’estimer ces coefficients locaux : HAPMIX (Price et al., 2009), EILA (J. J. Yang, Li, Buu, & Williams, 2013), LAMP (Thornton & Bermejo, 2014), Loter (Dias-Alves et al., in prep) ou encore RFMix (Maples, Gravel, Kenny, & Bustamante, 2013).

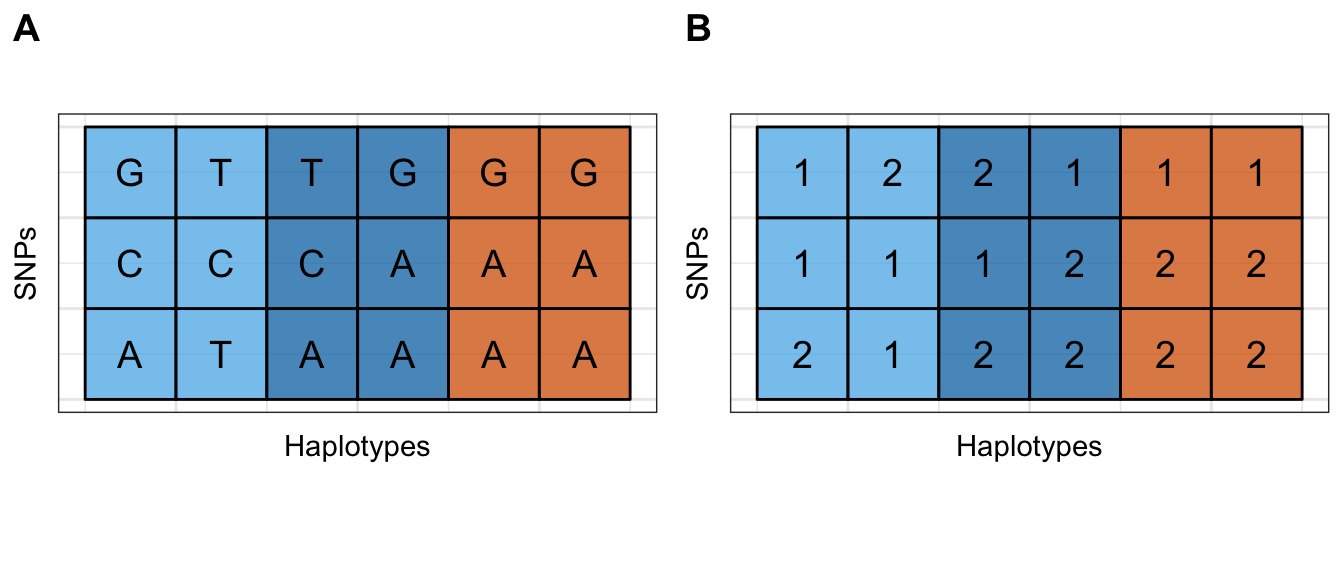
Figure 3.2: Exemple de matrice de coefficients de métissage locaux pour des individus issus du métissage de deux populations sources (numérotées 1 et 2). A. Chaque ligne de la matrice correspond à un SNP et chaque haplotype est représenté par une colonne. B. Matrice de coefficients de métissage locaux individuels. Pour chaque nucléotide d’un haplotype, les méthodes d’estimation de coefficients de métissage locaux vont chercher à attribuer ce nucléotide soit à la population 1 soit à la population 2.

3.1.2 Statistique de test

À partir de la matrice de coefficients de métissage locaux individuels, il est possible d’estimer pour un SNP donné la proportion d’allèles provenant de chacune des populations sources considérées. Pour estimer la proportion d’allèles provenant de la population \(i\) pour le locus \(j\), il suffit de calculer le nombre moyen de fois qu’un allèle observé sur le locus \(j\) a été attribué à la population \(i\) (un même individu présente deux allèles sur un locus donné (Figure 3.2)). Notant \(M\) la matrice de coefficients de métissage locaux individuels (Figure 3.2, panel B), \(G\) la matrice de génotypes (précisons que \(M\) a deux fois plus de colonnes que \(G\) car elle est de même dimension que la matrice des haplotypes) et \(n\) le nombre d’individus métissés, la proportion d’allèles \(p_{jk}\) provenant de la population \(P_k\) au locus \(j\) s’écrit :

\[\begin{equation} p_{jk} = \frac{1}{2n}\sum_{i=1}^n \left(\delta_{M_{i, 2j-1}}^k + \delta_{M_{i, 2j}}^k\right), \end{equation}\]

où \(\delta_x^k = 1\) si \(x=k\) et \(0\) sinon, \(j=1,\dots,p\) où \(p\) est le nombre de locus et \(k=1,\dots,K\) où \(K\) est le nombre de populations ancestrales. La proportion \(p_{jk}\) désigne le coefficient de métissage local au locus \(j\) à l’échelle de la population métisse. La recherche de régions d’introgression dans la population hybride se fait ensuite en regardant les coefficients de métissage locaux significativement élevés par rapport aux autres. Il n’y a pas de valeur standard pour le seuil de significativité, Suarez-Gonzalez (2016) choisissent par exemple un seuil de significativité de 3 écarts-types tandis que B. vonHoldt, Fan, Ortega-Del Vecchyo, Wayne, & others (2017) optent pour un seuil de significativité de 2 écarts-types.

3.2 Introgression par flux de gènes

La seconde classe de méthodes repose sur la comparaison de séquences de nucléotides, nucléotide par nucléotide. Un chromosome est par exemple divisé en un certain nombre de fenêtres (qui peuvent être disjointes ou chevauchantes), et les statistiques sont calculées sur chacune de ces fenêtres. Les séquences de nucléotides sont vues comme des chaînes de caractères et leur dissimilarité est mesurée à l’aide de distances classiques (ou de mesures de comptage) telles que la distance de Hamming.

3.2.1 Diversité nucléotidique par paires de séquences

Soient \(x = (x_i)_{1 \leq i \leq n}\) et \(y = (y_i)_{1 \leq i \leq n}\) deux séquences de nucléotides. En particulier, \(\forall i \in [|1, n|], \; x_i, y_i \in \{A, C, T, G \}\). La distance de Hamming \(d_{xy}\) entre la séquence \(x\) et la séquence \(y\) est définie par :

\[\begin{equation} d_{xy} = \text{Card}(\{i \in [|1, n|] \; | \; x_i \neq y_i \}). \end{equation}\]

Pour étudier les similarités localement sur le génôme à l’échelle de populations, deux mesures naturelles peuvent être constuites à partir de \(d_{xy}\), et consistent à calculer la distance moyenne et la distance minimale sur des séquences homologues provenant de différentes populations. Si \(X\) (resp. \(Y\)) désigne l’ensemble des séquences de la population \(P_1\) (resp. \(P_2\)), la distance moyenne et la distance minimale entre \(X\) et \(Y\) sont données par :

\[\begin{equation} \begin{split} d_{XY} &= \frac{1}{\text{Card}(X) \text{Card}(Y)}\sum_{x \in X} \sum_{y \in Y} d_{xy}, \\ d_{\min} &= \min_{(x,y) \in X \times Y} d_{xy}. \end{split} \end{equation}\]

\(d_{XY}\) est appelée la pairwise nucleotide diversity et estime le nombre moyen de nucléotides différents entre une séquence venant de la population \(X\) et une séquence venant de la population \(Y\). \(d_{\min}\) estime la distance minimale entre deux séquences tirées de \(P_1\) et de \(P_2\). Notons que \(d_{XY}\) et \(d_{\text{min}}\) étant symétriques, \(X\) et \(Y\) jouent des rôles équivalents, si bien que l’utilisation de ces distances pour détecter l’introgression ne permet pas de conclure sur le sens du flux de gènes que l’on cherche à mettre en évidence. De plus, pour détecter l’introgression entre deux populations \(X\) et \(Y\) à partir de distances entre séquences nucléotidiques, la seule donnée de \(d_{XY}\) ou de \(d_{\min}\) ne suffit pas, une distance n’étant une mesure de proximité que si elle est mise en comparaison avec une autre distance. C’est pour cela que les statistiques d’introgression basées sur ce type de distance requièrent généralement la donnée d’une population de contrôle \(O\) (appelée aussi outgroup). C’est le cas par exemple des statistiques \(RND\) (Feder et al., 2005) et \(RND\min\) (Rosenzweig, Pease, Besansky, & Hahn, 2016) définies ci-dessous :

\[\begin{equation} \begin{split} RND = \frac{2d_{XY}}{d_{XO} + d_{YO}}, \\ RND\min = \frac{2d_{\min}}{d_{XO} + d_{YO}}. \end{split} \end{equation}\]

Dans le cas de \(RND\min\), une séquence sera donc détectée comme étant introgressée pour de faibles valeurs de \(RND\min\).

3.2.2 Le modèle ABBA-BABA

L’emploi de ce modèle suppose l’accès à des séquences nucléotidiques provenant de quatre populations :

• une population donneuse.

• deux populations susceptibles de se reproduire avec la population donneuse.

• une population de contrôle avec qui toute possibilité de métissage est exclue.

Ces populations sont généralement présentées selon le schéma suivant (Figure 3.3) :

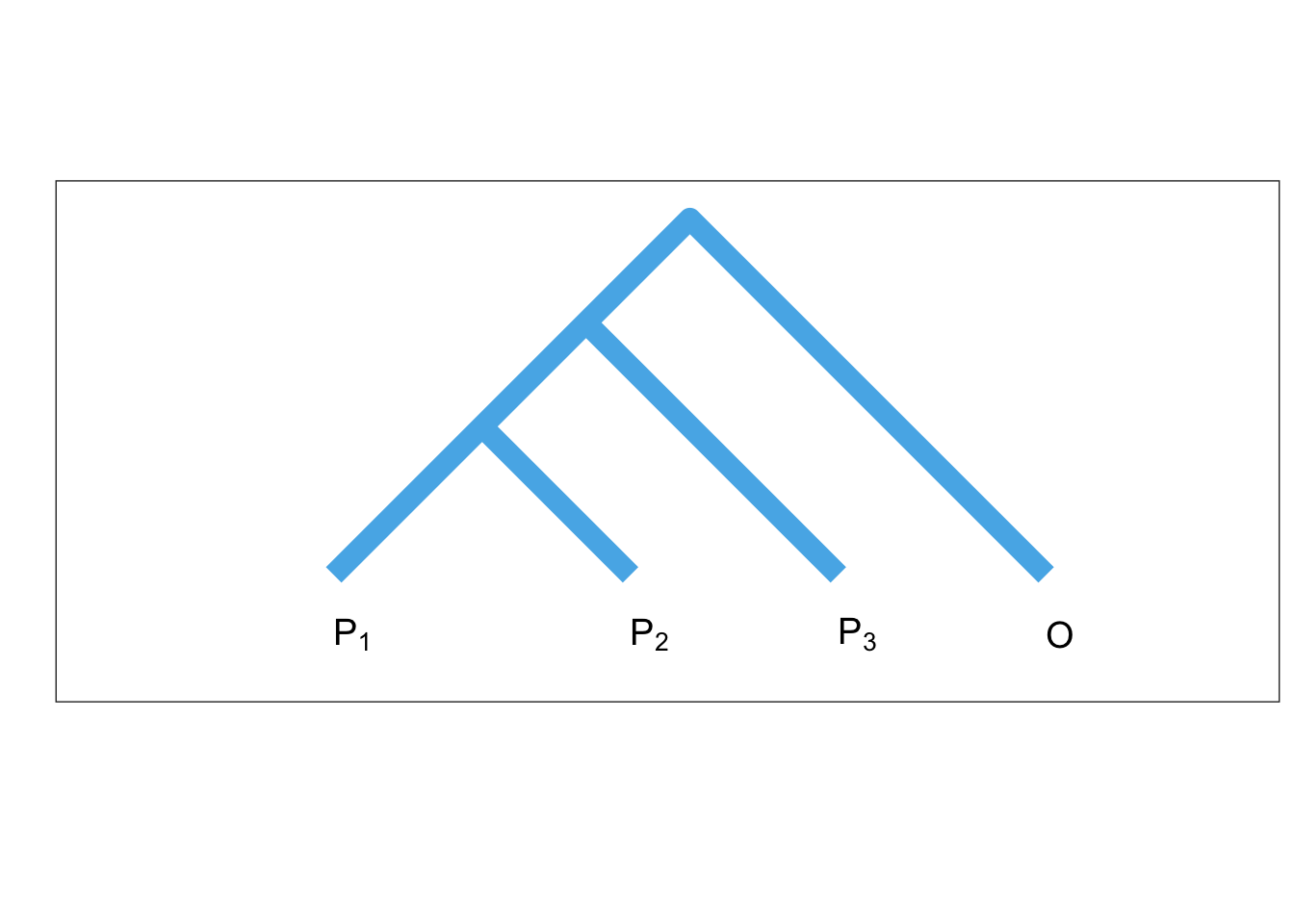
Figure 3.3: Arbre allélique. \(O\) désigne la population de contrôle, \(P_3\) la population donneuse, \(P_1\) et \(P_2\) les deux populations susceptibles de recevoir des allèles provenant de \(P_3\).

Sous l’hypothèse nulle, c’est-à-dire en l’absence d’introgression, la proportion de nucléotides communs à \(P_3\) et \(P_1\) doit être la même que la proportion de nucléotides communs à \(P_3\) et à \(P_2\). À l’inverse, un évènement d’introgression entre \(P_3\) et \(P_1\) devrait s’accompagner de l’augmentation de la fraction de séquences partagées par \(P_3\) et \(P_1\), relativement à \(P_2\). Cette différence de proportions est mesurée par la statistique \(D\) de Patterson (Durand, Patterson, Reich, & Slatkin, 2011), conçue spécifiquement pour détecter l’introgression de manière globale sur le génôme. De façon plus imagée, notant \(A\) et \(B\) respectivement les allèles portés par \(O\) et par \(P_3\), la statistique \(D\) compte le nombre de motifs \(ABBA\) (Figure 3.4) et le nombre de motifs \(BABA\) (Figure 3.4) et teste si les deux quantités sont significativement différentes l’une de l’autre.

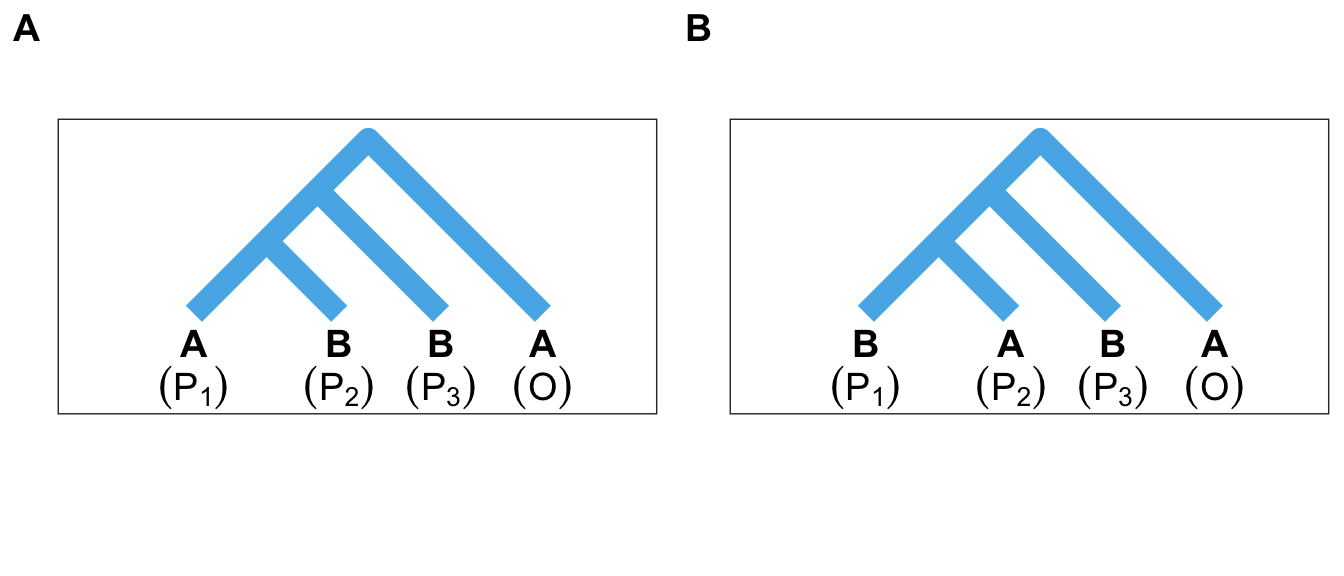
Figure 3.4: A. À gauche un arbre allélique présentant un motif \(ABBA\) indiquant que l’allèle \(B\) présent dans la population \(P_2\) a été hérité de la population \(P_3\). B. À droite un arbre allélique présentant un motif \(BABA\) indiquant que l’allèle \(B\) présent dans la population \(P_1\) a été hérité de la population \(P_3\).

La statistique \(D\) de Patterson, définie à partir des motifs \(ABBA\) et \(BABA\), est donnée par la relation suivante :

\[\begin{equation} D = \displaystyle \frac{\sum_i C_{ABBA}(i) - C_{BABA}(i)}{\sum_i C_{ABBA}(i) + C_{BABA}(i)} \end{equation}\]

où \(C_{ABBA}(i)\) (resp. \(C_{BABA}(i)\)) désigne le nombre de motifs \(ABBA\) (resp. \(BABA\)) observés sur le site \(i\). Selon S. H. Martin, Davey, & Jiggins (2014), cette statistique présente le défaut de trouver des outliers dans des régions à faible diversité allélique qui ne sont pas nécessairement introgressées. Partant de ce constat, de nombreuses variantes ont été développées à partir de cette statistique, dont les statistiques \(\text{Bd}_{f}\) (Pfeifer & Kapan, 2017) et \(f_d\) (S. H. Martin et al., 2014) auxquelles nous nous comparons, afin de corriger les défauts de la statistique \(D\).

3.3 Une nouvelle statistique pour les scans d’introgression

3.3.1 Analyse en Composantes Principales locale

Les méthodes de détection d’introgression que nous avons présentées, aussi bien dans un scénario de métissage que dans un scénario à flux de gènes (Figure 3.1), reposent sur le même principe, à savoir que dans une zone d’introgression les motifs observés diffèrent significativement de ce qui est observé à l’échelle globale (soit en termes de coefficients de métissage, soit en termes de motifs d’arbre allélique).

Nous proposons dans ce paragraphe d’utiliser les scores de l’ACP en tant que motif de comparaison, ceci étant justifié par le fait que le métissage à l’échelle du génôme peut être estimé à partir des scores des individus métissés (G. McVean, 2009). Notant \(B\) le barycentre des scores des individus d’une population métissée \(P\), et \(B_1\) (resp. \(B_2\)) le barycentre des scores des individus appartenant à la population \(P_1\) (resp. \(P_2\)), nous pouvons estimer la proportion globale de métissage de \(P\) relativement à \(P_1\) et \(P_2\) en calculant les coordonnées barycentriques de \(B\) dans le repère (\(B_1\), \(B_2\)), c’est-à-dire en déterminant les coefficients \(q_1\) et \(q_2\) tels que \(B = q_1 B_1 + q_2 B_2\) avec \(q_1 + q_2 = 1\).

À l’échelle locale, nous pourrions également définir de tels coefficients barycentriques, à la condition de pouvoir définir des scores locaux. Dans la littérature, nous trouvons deux façons de définir de tels scores :

• les scores de l’ACP réalisée sur des sous-ensembles de SNPs (H. Li & Ralph, 2016; B. vonHoldt et al., 2017). Cette approche revient à fenêtrer le génôme et à réaliser l’ACP sur chacune des fenêtres.

• les scores locaux de l’ACP. Cette approche consiste à déterminer les loadings en effectuant une ACP classique sur l’ensemble du génôme, puis les scores locaux sont obtenus en ne prenant en compte que les loadings de la fenêtre considérée. Dit autrement, cela revient à calculer les coefficients de la régression de \(\tilde{G}\) par un sous-ensemble de loadings \(\Sigma V^T\) où \(\tilde{G} \simeq U \Sigma V^T\) est la décomposition en valeurs singulières de la matrice de génotypes normalisée. Ces coefficients de régression sont par ailleurs appelés scores de métissage par Brisbin et al. (2012).

Nous choisissons ici d’utiliser la seconde approche basée sur les coefficients de régression, principalement parce que la première n’est pas adaptée au cas de données génétiques denses. Une approche par fenêtre glissante nécessiterait de réaliser un nombre d’ACP locales équivalent au nombre de marqueurs présents, soit une complexité en \(O(np^2)\) (où \(n\) désigne le nombre d’individus et \(p\) le nombre de marqueurs génétiques), contrairement à la seconde méthode qui peut être implémentée en temps linéaire par rapport à \(n\) et à \(p\). Notant \(i\) un entier compris entre \(1\) et \(p\), et \(x_i\) la position génétique (mesurée en Morgans) ou la position physique (mesurée en paires de bases) du \(i\)-ème marqueur génétique. Nous définissons pour cet entier \(i\) la fenêtre \(W_i^T\) de taille \(T\) et centrée en \(i\) par :

\[\begin{equation} W_i^T = \{ j \in [|1, p|], |x_i - x_j| \leq T/2 \} \end{equation}\]

Soit \(\tilde{G} = U \Sigma V^T\) la décomposition en valeurs singulières de la matrice de génotypes normalisée \(\tilde{G}\). Partant de l’approximation \(U \simeq \tilde{G}V\Sigma^{-1}\), les scores de métissage sont définis de la façon suivante (Brisbin et al., 2012) :

\[\begin{equation} U_{W_i^T} = \tilde{G}_{.,W_i^T}V_{W_i^T,.}\Sigma^{-1} \end{equation}\]

Les proportions de métissage local de la population \(B_{W_i^T}\) sont définies de la même façon que dans le cas global, à la différence qu’elles utilisent les scores locaux \(U_{W_i^T}\) à la place des scores globaux \(U\). Ainsi, une région sera considérée comme potentiellement introgressée si les proportions de métissage locale calculées sur cette région sont significativement différentes des proportions de métissage calculées à l’échelle du génôme.

Calcul des scores locaux

Si nous calculions \(U_{W_i^T}\) pour chaque valeur de \(i\) de façon naïve, la complexité algorithmique de cette étape serait en \(O(nKp^2)\). Pour réduire cette complexité, l’idée est d’exploiter le fait que les fenêtres \(W_i^T\) et \(W_{i+1}^T\) se chevauchent, ce qui permet de déduire \(U_{W_{i+1}^T}\) à partir de \(U_{W_i^T}\) en effectuant moins d’opérations que n’en nécessiterait le calcul individuel de \(U_{W_{i+1}^T}\).

3.3.2 Résultats principaux

Nous proposons une méthode spécifiquement dédiée à la détection d’introgression. Le développement d’une méthode destinée spécifiquement à la détection d’introgression est motivé par le fait que les méthodes basées sur l’estimation de coefficients de métissage nécessitent de disposer d’informations parfois difficiles à obtenir comme la phase des haplotypes. Le problème de la détection d’introgression étant plus simple que celui de l’estimation des coefficients de métissage locaux, nous proposons une approche qui permet de s’affranchir d’étapes relativement lourdes telles que la détermination des haplotypes et de leur phase, allégeant considérablement le temps de calcul nécessaire. À l’aide de simulations numériques réalisées pour les deux types de scénarios d’introgression présentés, nous montrons que notre statistique produit un taux de fausses découvertes et une puissance comparables aux méthodes de l’état de l’art (Figure 3.7), en utilisant seulement la donnée de génotypes.

Application au jeu de données de peupliers. Nous avons testé notre méthode sur un jeu de données de peupliers d’Amérique du Nord (Suarez-Gonzalez, 2016). Deux populations de peupliers ont été génotypées, Populus balsamifera qui est une population adaptée aux conditions boréales et Populus trichocarpa qui est une population adaptée au climat doux du Nord-Ouest américain (Suarez-Gonzalez, 2016). Comme Suarez-Gonzalez (2016), nous avons regardé, chez les individus métisses avec une ascendance génétique Trichocarpa majoritaire, les régions de leur génôme présentant un excès d’ascendance génétique Balsamifera qui leur permet de s’adapter à des conditions plus froides et sèches. Nous trouvons la même région d’introgression sur le chromosome 6 que Suarez-Gonzalez (2016) (Figure 3.5). Sur le chromosome 15 nous trouvons également les mêmes régions candidates. En revanche, nous trouvons deux nouvelles régions candidates sur le chromosome 12 (Figure 3.6), qui sont également détectées par RFMix (Maples et al., 2013). L’une d’entre elles est également détectée avec Loter. Cette différence de résultats peut être due au prétraitement des données de génotypes. Suarez-Gonzalez (2016) ont appliqué des filtres enlevant près de \(95\%\) du jeu de données initial. De notre côté, nous avons choisi de filtrer les SNPs ayant plus de \(5\%\) de données manquantes, ce qui permettait de conserver plus de \(70\%\) du jeu de données initial.

Figure 3.5: Résultats du scan d’introgression obtenus sur le chromosome 6 du jeu de données de peupliers (Suarez-Gonzalez, 2016) avec différentes méthodes basées sur l’estimation des coefficients de métissage locaux.

Figure 3.6: Résultats du scan d’introgression obtenus sur le chromosome 12 du jeu de données de peupliers (Suarez-Gonzalez, 2016) avec différentes méthodes basées sur l’estimation des coefficients de métissage locaux.

Résultats sur des simulations de modèle de métissage. Pour quantifier les performances de chaque méthode basée sur l’estimation des coefficients de métissage locaux, nous avons réalisé des simulations à partir du jeu de données de peupliers décrit ci-dessus (Suarez-Gonzalez, 2016). La simulation d’haplotypes d’individus métissés est réalisée à partir des deux populations ancestrales qui y sont présentes. Chacune des simulations est constituée de \(50\) haplotypes de la souche continentale, de \(50\) haplotypes de la souche boréale, ainsi que de \(50\) haplotypes d’individus hybrides générés à partir des haplotypes ancestraux. Ces haplotypes ancestraux ont été estimés à l’aide du logiciel Beagle (S. R. Browning & Browning, 2007). En suivant une procédure que nous ne décrivons pas ici (cf. article 3), nous choisissons pour chaque simulation, de façon aléatoire, une région qui sera sujette à un évènement d’introgression. Nous donnons en figure 3.7 une comparaison des résultats obtenus avec les différents logiciels d’estimation des coefficients de métissage locaux. Nous constatons que notre méthode, basée uniquement sur l’information génotypique, obtient des résultats similaires aux méthodes nécessitant la donnée d’haplotypes.

Figure 3.7: Proportion de régions effectivement introgressées sur les 5 régions jugées les plus significatives pour chaque méthode (EILA, Loter, RFMix et pcadapt) dans un scénario de métissage à deux populations. L’intensité de l’introgression est paramétrée par la variable \(\Delta_q\) donnée en abscisse. De gauche à droite, le résultat de la comparaison pour des épisodes de métissage survenus il y a respectivement 1000, 100 et 10 générations.

Résultats sur des simulations de modèle de flux de gènes. De la même manière, pour évaluer notre méthode dans un scénario à flux de gènes, nous reprenons les modèles de simulation proposés par S. H. Martin et al. (2014). L’idée est la même que précédemment. À l’aide de ces modèles nous générons des séquences de nucléotides pour quatre populations \(P_1\), \(P_2\), \(P_3\), et \(O\) dont l’histoire démographique est celle racontée en figure 3.3. Pour la population receveuse \(P_2\), nous choisissons une région dans laquelle les séquences de \(P_2\) sont mélangées à des séquences de la population donneuse \(P_3\), simulant de cette manière un évènement d’introgression. Les résultats de cette comparaison sont donnés en figure 3.8. Nous constatons que dans le cas où le taux de mutation est constant le long du génôme, notre méthode obtient des performances similaires aux autres méthodes. En revanche, dans le cas où le taux de mutation est variable, elle semble être la moins robuste de toutes.

Figure 3.8: Proportion de régions effectivement introgressées sur les 5 régions jugées les plus significatives pour chaque méthode (\(\text{Bd}_f\), \(D\), \(f_d\), pcadapt, \(RND_{\text{min}}\)) dans un scénario à flux de gènes. Ici l’intensité de l’introgression est paramétrée par la variable \(f\).

3.4 Article 3

Scanning genomes for adaptive introgression using principal component analysis

Keurcien Luu, Thomas Dias-Alves & Michael G.B. Blum

Introduction

A potential source of adaptive genetic variation is adaptive introgression. Adaptive introgression occurs when selectively beneficial alleles are transferred between species (M. L. Arnold & Martin, 2009; Dasmahapatra et al., 2012; Fraïsse, Roux, Welch, & Bierne, 2014). Although adaptive genetic variation originates primarily from de novo mutation or standing variation, adaptive introgression is now acknowledged as an important source of genetic variation in plants but also in animals (Hedrick, 2013).

To model adaptive introgression, there are at least two conceptual evolutionary scenarios. In the first “admixture” scenario, two populations or two related species admixed to form a new hybrid population (Figure 3.9). Adaptive introgression occurs when variation from one of the source population is adaptive in the environment of the admixed population. For instance, Tibetans are the result of admixture between Han and Sherpa populations, and alleles that confer adaptation to high altitude have been transmitted by the Sherpa population (Jeong et al., 2014). Evidence of adaptive introgression following admixture has been provided in several admixed populations or species, including Africanized honeybee, Populus species, North American canids, or human Bantu-speaking populations to name just a few examples (R. M. Nelson, Wallberg, Simões, Lawson, & Webster, 2017; Patin et al., 2017; Payseur & Rieseberg, 2016; Suarez-Gonzalez, 2016; B. M. vonHoldt, Kays, Pollinger, & Wayne, 2016). The second evolutionary scenario assumes “gene flow” or “introgression” from a donor species to an introgressed species (Figure 3.9). For instance, house mice became resistant to a warfarin pesticide because of selection on VKORC1 polymorphisms that have been acquired from the Algerian mouse (M. spretus) through introgression (Y. Song et al., 2011). Another classical example of introgression followed by adaption include colour adaptations in Heliconius species (Pardo-Diaz et al., 2012). Whereas detection of loci involved in adaptive introgression are performed with different statistical methods for the admixture and gene flow evolutionary models, we propose a statistical approach that is valid in both evolutionary models.

In the admixture model, outlier loci are found by looking for genomic regions harboring excess of ancestry from the donor population (Buerkle & Lexer, 2008). Excess of ancestry are obtained using local ancestry inference (LAI) that computes for admixed individuals the number of chromosome copies coming from the ancestral populations. There are several software available for LAI including EILA, HAPMIX, LAMP-LD, or RFMix (Baran et al., 2012; Jeong et al., 2014; Maples et al., 2013; Price et al., 2009). Except for EILA, LAI software can require biological information that can be difficult to obtain especially for non-model species. For instance, HAPMIX or RFMix require phased haplotypes for the ancestral populations and RFMix also require phased haplotypes for the admixed individuals. In addition, a recombination map and an estimate of the admixture date between the ancestral populations should be provided for both HAPMIX and RFMix (Baran et al., 2012; Jeong et al., 2014; Maples et al., 2013; Price et al., 2009).

In the “gene flow” or “introgression” scenario, there have also been attempts to find introgressed regions with outlier detection methods (Rheindt, Fujita, Wilton, & Edwards, 2013; Smith & Kronforst, 2013; W. Zhang, Dasmahapatra, Mallet, Moreira, & Kronforst, 2016). A common approach is to test for an excess of shared derived variants in the donor and recipient populations using the \(D\) or ABBA-ABBA test statistic (Durand et al., 2011). However, extreme \(D\) values occur disproportionately in genomic regions with lower diversity (S. H. Martin et al., 2014). Because genome scans with the \(D\) statistic generate too many false positives, more powerful statistics have been developed such as the \(f_d\) or \(\text{Bd}_f\) statistic (S. H. Martin et al., 2014; Pfeifer & Kapan, 2017). In addition, the \(D\) statistic and its extensions cannot be used to identify introgressed regions between sister species (see Figure 3.9); it should be used with three or more lineages to detect the different topologies produced by hybridization (Rosenzweig et al., 2016). To identify introgression between sister species, various alternative statistics have been developed including \(RND_{\text{min}}\), which computes the minimum pairwise distance between the two sister species relative to the divergence to an outgroup. In contrast to the \(D\) statistic and its extension, \(RND_{\text{min}}\) requires phased data (Rosenzweig et al., 2016).

We propose a statistical method to detect candidates for adaptive introgression that is valid in both the admixture scenario and the introgression scenario. The proposed approach is based on principal component analysis (PCA), which is well-suited to ascertain population structure of large scale genome-wide dataset (G. McVean, 2009; N. Patterson et al., 2006). Numerical solutions to compute principal component scores can be obtained rapidly even with large scale data (Abraham, Qiu, & Inouye, 2017; Duforet-Frebourg et al., 2015; Galinsky et al., 2016). The proposed approach does not require any biological information in addition to the genome-wide genotype data and should therefore be valuable especially for non-model species where recombination map are not available and where haplotype phasing can be a daunting task. The statistical method we propose ascertains population structure locally in the genome by computing local principal components. Candidate SNPs for local introgression correspond to genomic regions for which population structure of the admixed or introgressed population deviates significantly from genome-wide population structure (Figure 3.9). To capture population structure of the admixed or introgressed individuals with respect to the other individuals, the method computes an average ancestry coefficient. In the following, we investigate to what extent the PCA-based approach provides an alternative to LAI and to the aforementioned phylogenetic statistics in the admixture and introgression scenario. We show the potential of the method to detect adaptive introgression in a hybrid Populus species resulting from a 2-way admixture model (Suarez-Gonzalez, 2016). The PCA-based method is implemented in the R package pcadapt (Luu et al., 2017).

A PCA-based approach to detect local introgression

The objective of PCA is to find a new set of orthogonal variables called the principal components, which are linear combinations of (centered and standardized) allele counts, such that the projections of the data onto these axes lead to an optimal summary of the data. To present the method, we introduce the truncated singular value decomposition (SVD) that approximates the \((n \times p)\) centered and scaled genotype matrix \({\bf Y}\) by a matrix of smaller rank

\[\begin{equation} {\bf Y}\approx{\bf U}{\bf \Sigma} {\bf V}^T, \tag{3.1} \end{equation}\]

where \({\bf U}\) is a \((n \times K)\) orthonormal matrix, \({\bf V}\) is a \((p \times K)\) orthonormal matrix, \({\bf \Sigma}\) is a diagonal \((K \times K)\) matrix and \(K\) corresponds to the rank of the approximation. The solution of PCA with \(K\) components can be obtained using the truncated SVD of equation (3.1): the \(K\) columns of \({\bf V}\) contain the loadings, which correspond to the contribution of each SNP to the PCs and the \(K\) columns of \({\bf U}\) contain the PC scores that are usually displayed to visualize population structure (Duforet-Frebourg et al., 2015; N. Patterson et al., 2006).

To provide local measure of population structure, we compute local PCA scores. For a SNP \(j\), we compute the vector of local scores \({\bf U_j}\) that measure population structure locally in the genome

\[\begin{equation} {\bf U}_j = {\bf Y_j}{\bf V_j}{\bf \Sigma}^{-1}, \tag{3.2} \end{equation}\]

where \({\bf Y_j}\) correspond to the genotype restrained to a genomic window around SNP \(j\) and \({\bf V_j}\) corresponds to the loadings restrained to a genomic window around SNP \(j\).

An average local ancestry coefficient \(q\) is then obtained from the local scores \({\bf U}_j\) using barycentric coordinates for the barycenter \(B\) of the local scores of admixed or introgressed individuals. Barycentric coordinates of \(B\) correspond to the \(K\) coefficients \(q_1, \dots, q_K\) (\(q_1+\dots+q_K=1\)) such that \(B\) can be written as a linear combination \(B = q_1 B_1 + \dots + q_K B_K\) where \(B_1, \dots, B_K\) are the barycenters of local scores for the \(K\) source populations. In the admixture scenario, barycentric coordinates are always between 0 and 1 because local scores of admixed individuals are always contained in the simplex determined by the barycenters of the ancestral populations (Figure B.29). By contrast, barycentric coordinates can be negative or larger than 1 for the introgression scenario (B.28). To find outlier regions with excess of ancestry from the donor population \(j\) that is one of the \(K\) source populations, we compute robust mean \(\mu_j\) and variance \(\sigma^2_j\) of the average ancestry coefficients using the median absolute deviation and we consider the standardized average ancestry coefficient \((q_j - \mu_j) / \sigma_j\), \(j = 1, \dots, K\).

Materials and Methods

Parameter settings for local ancestry and adaptive introgression software

For the admixture scenario, we consider three software of local ancestry inference, which are EILA, Loter and RFMix (Maples et al., 2013; J. J. Yang et al., 2013). EILA considers genotypes as input and we consider a regularization parameter of \(\lambda=0.1\). Loter uses haplotypes as input data and has no tuning parameter. RFMix uses haplotypes as input data and we consider the default parameter except the window size that was set at 0.002cM. Using the default window size generates an error and as recommended by the manual of RFMix, we reduce window size to overcome this issue. When analyzing Populus data, we consider the same averaging strategy as implemented in the initial analysis with RASPberry and average local ancestry coefficients obtained with RFMix and Loter using 100kbp windows (Suarez-Gonzalez, 2016).

For the introgression scenario, we compared pcadapt to the \(\text{Bd}_f\), \(D\), \(f_d\), and \(RND_{\text{min}}\) test statistics (Durand et al., 2011; S. H. Martin et al., 2014; Pfeifer & Kapan, 2017; Rosenzweig et al., 2016). The \(D\), \(\text{Bd}_f\) and \(f_d\) statistics require genotype data for the three related species as well as from an outgroup species, for which we also simulate genotypes. Because \(RND_{\text{min}}\) tests for introgression between sister species, we provide sequence (haplotype) data from 3 species, which are the introgressed, and donor species as well as an outgroup species (Figure 3.9). When using pcadapt, we provide genotype data from three species, which are introgressed, donor and sister species (Figure 3.9).

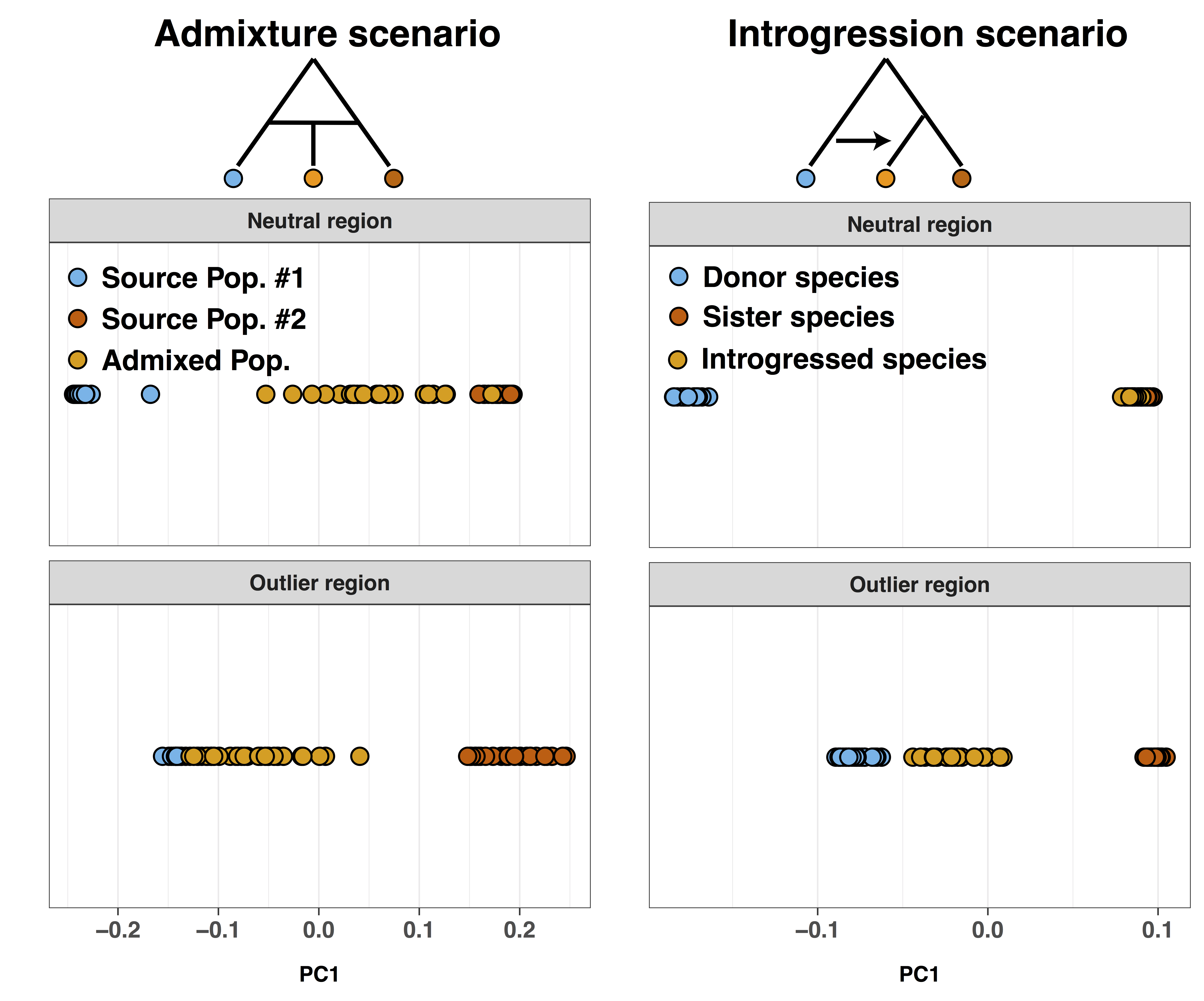
Figure 3.9: Principal components obtained for a neutral region and an outlier region in the admixture scenario (left panels) and in the introgression scenario (right panels). For the admixture scenario, simulations use phased genotype data from P. balsamifera and P. trichocarpa individuals and we assume that the difference \(\Delta_q\) of ancestry between outlier and neutral regions is of \(50\%\) and that admixture took place \(\lambda = 100\) generations ago. For the introgression scenario, the gene flow parameter \(f = 0.5\).

Simulations under an admixture scenario

We consider the example of admixture of two Populus species in North America to simulate admixed individuals (Suarez-Gonzalez, 2016). We considered genotypes from chromosome 6 of \(25\) individuals from the species Populus balsamifera (balsam poplar) and \(25\) individuals from the species Populus trichocarpa (black cottonwood) (Suarez-Gonzalez, 2016). In order to generate admixed individuals, we phase the 50 genotypes using Beagle (S. R. Browning & Browning, 2007). To construct admixed genomes, we began at the first marker on each chromosome and sampled Populus balsamifera ancestry with probability \(\alpha=70\%\) and Populus trichocarpa ancestry with probability \((1 - \alpha) = 30\%\). Haplotype of the admixed genome was form by sampling at random one of the haplotype coming from the P. balsamifera or P. trichocarpa species. Ancestry was resampled based on an exponential distribution with weight \(\lambda\), which corresponds to the number of generations since admixture (Price et al., 2009). A new ancestry tract was sampled with probability \(1 - e^{-\lambda g}\) when traversing a genetic distance of \(g\) Morgans. Each time ancestry was resampled, we sampled P. balsamifera ancestry with probability \(\alpha = 70\%\) and P. trichocarpa ancestry with probability \((1 - \alpha) = 30\%\). In the simulations, we consider the first \(100,000\) SNPs of the chromosome 6 of Populus individuals. To model adaptive introgression, we assume that there is a region containing \(1,000\) SNPs where P. balsamifera ancestry was equal to \(70\%-\Delta_q\) instead of \(70\%\). We consider different values for \(\Delta_q\) which are equal to \(5\%\), \(10\%\), \(15\%\), \(20\%\), \(30\%\), \(40\%\), or \(50\%\). Simulations correspond to a model of soft sweep where different alleles of P. balsamifera ancestry, which span the \(500\) SNPs genomic regions, are adaptive (Messer & Petrov, 2013). Because there is no recombination map available in Populus, we assume a constant recombination rate of 0.05cM/Mbp (Suarez-Gonzalez, 2016). We consider three different values for the time since admixture \(\lambda\), which is equal to \(10\), \(100\), or \(1000\) generations. For each value of \(\lambda\) and of \(\Delta_q\), we generate \(50\) replicates containing \(25\) admixed individuals each. When looking for adaptive introgression in admixed P. trichocarpa individuals, we consider SNPs with less than \(5\%\) of missing values typed in \(36\) admixed individuals (Suarez-Gonzalez, 2016).

Simulations under an introgression scenario

We consider simulations of introgression as described by (S. H. Martin et al., 2014). To simulate genomes, we concatenate 45 \(5,000\) bp regions without introgression and 5 \(5,000\) bp regions where each individuals from the introgressed species is drawn from the donor population with a probability \(f\) (Supplementary Figure B.28). The parameter \(f\) measures the extent of introgression for introgressed regions. When \(f = 1\) all individuals from the introgressed species come from the donor population and \(f = 0\) correspond to the genomic windows without introgression. The ms command lines for simulating neutral and introgressed (\(f = 20\%\)) regions for \(25\) individuals in each population are given as follows (Hudson, 2002)

Sequence data were then generated using the software Seq-Gen using the Hasegawa-Kishino-Yano substitution model and a branch scaling factor of 0.01 (./seq-gen -mHKY -l 5000 -s 0.01) (Rambaut & Grass, 1997).

Evaluation rules for simulations

For admixture scenarios, we consider the 50,000 first SNPs of chromosome 6 when evaluating different software. To evaluate statistical power, we consider 50 windows containing 1,000 SNPs each. To compute a score for each window, we consider two methods: averaging ancestry coefficients over all SNPs within a window or considering the maximum of ancestry coefficients within a window. For a fixed number of regions considered as outliers, we report statistical power defined as the average over simulations of the number of detected outlier regions divided by five, which is the true number of outlier regions.

For introgression scenarios, we simulated 50 windows of \(5,000\) bp. All statistics but pcadapt are computed using \(5,000\) bp windows. Statistical power is returned when considering the 5 top hits, which corresponds to the 5 largest values of the test statistics.

Results

Simulations under an admixture scenario

For a simulated admixture scenario between two Populus species, we display standardized ancestry coefficients computed by pcadapt and LAI software (Supplementary Figure B.23). When simulating admixed individuals, we assume that there are five outlier regions where the amount of P. trichocarpa ancestry is increased by an amount of \(\Delta_q\) compared to other regions. In the genome scans shown in figure B.23, the top 5 peaks obtained with all software correspond to the peaks that should be detected. The power of LAI software based on haplotypes (Loter and RFMix), when varying values of \(\Delta_q\) and of \(\lambda\), is comparable to the power obtained by an ideal method called oracle, which would know ancestry chunks for each admixed individual (Figure 3.10). For Loter, the loss of power—averaged over \(\Delta_q\)—is comprised between \(1\%\) and \(19\%\) depending on the number of generations since admixture (Supplementary Figure B.24). For RFMix, the loss of power is comprised between \(3\%\) and \(11\%\). When considering methods based on genotypes, we find that the power obtained with EILA is considerably reduced compared to an oracle because loss of power is always larger than \(55\%\). When considering other values of the regularization parameter \(\lambda\) for EILA, statistical power was further reduced. By contrast, the power of pcadapt is comparable to the power obtained with haplotype-based methods. Compared to an oracle, the loss of power of pcadapt is comprised between \(3\%\) and \(7\%\). The power of pcadapt is increased compared to haplotype-based methods for ancient admixture events (\(\lambda=1,000\) generations) whereas it is decreased for recent admixture events (\(\lambda=10\) generations) (Figure 3.10). Because we evaluate statistical power on a genomic region-by-region basis, we had to define a compound ancestry measure for each genomic region and figure 3.10 corresponds to results obtained when considering the average ancestry coefficient within each genomic region. If we rather compute the maximum of ancestry coefficients within each window, the power of pcadapt is again increased compared to haplotype-based methods for ancient admixture events whereas results are more balanced for recent admixture events (Supplementary Figure B.25). Although pcadapt considers genotypes only, we find that it provides statistical power comparable to LAI software that make use of haplotypes. When considering additional hits to the five top hits, the statistical power of pcadapt is again comparable to the one obtained with haplotype-based methods (Supplementary Figure B.26).

Figure 3.10: Proportion of true outlier peaks among the five top peaks found with pcadapt and different LAI methods (EILA, Loter and RFMix) in a scenario where 2 Populus populations experienced admixture. Proportion of true outlier peaks is displayed as a function of the difference \(\Delta_q\) of ancestry between outlier and neutral regions. The three panels correspond to the three different possible values (\(\lambda=10\) or \(100\) or \(1000\)) of the number of generations since admixture.

Adaptive introgression in Populus admixed individuals

We replicated the search for adaptive introgression in admixed Populus species (Suarez-Gonzalez, 2016). We searched for genomic regions with excess of P. balsamifera ancestry (boreal species) in admixed P. trichocarpa individuals (temperate species). We compare outlier regions found with RFMix, pcadapt and Loter to the regions already found by Suarez-Gonzalez (2016) with the software RASPberry, which implements the HAPMIX model for local ancestry. All software found the peak in chromosome 6 that is located 3.36Mb away from the start of the chromosome (Suarez-Gonzalez, 2016).

Simulations under an introgression scenario

We compared power of several introgression statistics in introgression scenarios. When the proportion \(f\) of introgression for introgressed region is equal to 1, all individual from the introgressed population descend from the donor population. In this situation of massive introgression, the power of all statistics is equal to \(100\%\) except for the \(D\) statistics, which has a power of \(94\%\) (Figure B.27). The power of all statistics remains at \(100\%\) when \(f \geq 0.7\) except the \(D\) statistic whose power decreases to \(80\%\) for \(f = 80\%\). When \(f\) further decreases, powers of all statistics also decrease with the \(D\) statistics being the less powerful statistic. The more powerful statistics is \(RND_{\text{min}}\), followed by \(f_d\), \(\text{Bd}_f\), and pcadapt. For the most difficult scenarios where \(f = 5\%\), the power of \(RND_{\text{min}}\) is \(68\%\), the power of \(f_d\) is \(64\%\), the power of \(\text{Bd}_f\) is \(60\%\), the power of pcadapt is \(56\%\) and the power of \(D\) is \(38\%\).

We consider Populus simulated admixed individuals to evaluate if the PCA-based approach manages to identify true outliers for local ancestry. By considering the 5 peaks with highest values of local ancestry, we compare statistical power obtained with the PCA-based approach and with LAI software. For each software, statistical power decreases as a function of \(\Delta_q\) as it was expected (Figure 3.10). Among all software we consider, RFMix and Loter maximize statistical power whatever the value of the time since admixture \(\lambda\) and of the difference of allele frequency between introgressed and non-introgressed regions (Figure 3.10). Although the power of the PCA approach is reduced, the loss of power is very small when compared to RFMix or Loter. By contrast, the reduction of power obtained with EILA, which is another method that use genotype only, is considerable.

References

Hedrick, P. W. (2013). Adaptive introgression in animals: Examples and comparison to new mutation and standing variation as sources of adaptive variation. Molecular Ecology, 22(18), 4606–4618.

Alexander, D. H., Novembre, J., & Lange, K. (2009). Fast model-based estimation of ancestry in unrelated individuals. Genome Research, 19(9), 1655–1664.

Frichot, E., & François, O. (2015). LEA: An r package for landscape and ecological association studies. Methods in Ecology and Evolution, 6(8), 925–929.

Caye, K., Deist, T. M., Martins, H., Michel, O., & François, O. (2016). TESS3: Fast inference of spatial population structure and genome scans for selection. Molecular Ecology Resources, 16(2), 540–548.

Suarez-Gonzalez, et a., Adriana. (2016). Genomic and functional approaches reveal a case of adaptive introgression from populus balsamifera (balsam poplar) in p. trichocarpa (black cottonwood). Molecular Ecology, 2427–2442.

Price, A. L., Tandon, A., Patterson, N., Barnes, K. C., Rafaels, N., Ruczinski, I., … Myers, S. (2009). Sensitive detection of chromosomal segments of distinct ancestry in admixed populations. PLoS Genetics, 5(6), e1000519.

Yang, J. J., Li, J., Buu, A., & Williams, L. K. (2013). Efficient inference of local ancestry. Bioinformatics, 29(21), 2750–2756.

Thornton, T. A., & Bermejo, J. L. (2014). Local and global ancestry inference and applications to genetic association analysis for admixed populations. Genetic Epidemiology, 38(S1).

Maples, B. K., Gravel, S., Kenny, E. E., & Bustamante, C. D. (2013). RFMix: A discriminative modeling approach for rapid and robust local-ancestry inference. The American Journal of Human Genetics, 93(2), 278–288.

vonHoldt, B., Fan, Z., Ortega-Del Vecchyo, D., Wayne, R. K., & others. (2017). EPAS1 variants in high altitude tibetan wolves were selectively introgressed into highland dogs. PeerJ, 5, e3522.

Feder, J. L., Xie, X., Rull, J., Velez, S., Forbes, A., Leung, B., … Aluja, M. (2005). Mayr, dobzhansky, and bush and the complexities of sympatric speciation in rhagoletis. Proceedings of the National Academy of Sciences, 102(suppl 1), 6573–6580.

Rosenzweig, B. K., Pease, J. B., Besansky, N. J., & Hahn, M. W. (2016). Powerful methods for detecting introgressed regions from population genomic data. Molecular Ecology, 25(11), 2387–2397.

Durand, E. Y., Patterson, N., Reich, D., & Slatkin, M. (2011). Testing for ancient admixture between closely related populations. Molecular Biology and Evolution, 28(8), 2239–2252.

Martin, S. H., Davey, J. W., & Jiggins, C. D. (2014). Evaluating the use of abba–BABA statistics to locate introgressed loci. Molecular Biology and Evolution, 32(1), 244–257.

Pfeifer, B., & Kapan, D. D. (2017). Estimates of introgression as a function of pairwise distances. bioRxiv, 154377.

McVean, G. (2009). A genealogical interpretation of principal components analysis. PLoS Genetics, 5(10), e1000686.

Li, H., & Ralph, P. (2016). Local pca shows how the effect of population structure differs along the genome. bioRxiv, 070615.

Brisbin, A., Bryc, K., Byrnes, J., Zakharia, F., Omberg, L., Degenhardt, J., … Bustamante, C. D. (2012). PCAdmix: Principal components-based assignment of ancestry along each chromosome in individuals with admixed ancestry from two or more populations. Human Biology, 84(4), 343–364.

Browning, S. R., & Browning, B. L. (2007). Rapid and accurate haplotype phasing and missing-data inference for whole-genome association studies by use of localized haplotype clustering. The American Journal of Human Genetics, 81(5), 1084–1097.

Arnold, M. L., & Martin, N. H. (2009). Adaptation by introgression. Journal of Biology, 8(9), 82.

Dasmahapatra, K. K., Walters, J. R., Briscoe, A. D., Davey, J. W., Whibley, A., Nadeau, N. J., … others. (2012). Butterfly genome reveals promiscuous exchange of mimicry adaptations among species. Nature, 487(7405), 94.

Fraïsse, C., Roux, C., Welch, J. J., & Bierne, N. (2014). Gene-flow in a mosaic hybrid zone: Is local introgression adaptive? Genetics, 197(3), 939–951.

Jeong, C., Alkorta-Aranburu, G., Basnyat, B., Neupane, M., Witonsky, D. B., Pritchard, J. K., … Di Rienzo, A. (2014). Admixture facilitates genetic adaptations to high altitude in tibet. Nature Communications, 5, 3281.

Nelson, R. M., Wallberg, A., Simões, Z. L. P., Lawson, D. J., & Webster, M. T. (2017). Genome-wide analysis of admixture and adaptation in the africanized honeybee. Molecular Ecology.

Patin, E., Lopez, M., Grollemund, R., Verdu, P., Harmant, C., Quach, H., … others. (2017). Dispersals and genetic adaptation of bantu-speaking populations in africa and north america. Science, 356(6337), 543–546.

Payseur, B. A., & Rieseberg, L. H. (2016). A genomic perspective on hybridization and speciation. Molecular Ecology, 25(11), 2337–2360.

vonHoldt, B. M., Kays, R., Pollinger, J. P., & Wayne, R. K. (2016). Admixture mapping identifies introgressed genomic regions in north american canids. Molecular Ecology, 25(11), 2443–2453.

Song, Y., Endepols, S., Klemann, N., Richter, D., Matuschka, F.-R., Shih, C.-H., … Kohn, M. H. (2011). Adaptive introgression of anticoagulant rodent poison resistance by hybridization between old world mice. Current Biology, 21(15), 1296–1301.

Pardo-Diaz, C., Salazar, C., Baxter, S. W., Merot, C., Figueiredo-Ready, W., Joron, M., … Jiggins, C. D. (2012). Adaptive introgression across species boundaries in heliconius butterflies. PLoS Genetics, 8(6), e1002752.

Buerkle, C. A., & Lexer, C. (2008). Admixture as the basis for genetic mapping. Trends in Ecology & Evolution, 23(12), 686–694.

Baran, Y., Pasaniuc, B., Sankararaman, S., Torgerson, D. G., Gignoux, C., Eng, C., … others. (2012). Fast and accurate inference of local ancestry in latino populations. Bioinformatics, 28(10), 1359–1367.

Rheindt, F. E., Fujita, M. K., Wilton, P. R., & Edwards, S. V. (2013). Introgression and phenotypic assimilation in zimmerius flycatchers (tyrannidae): Population genetic and phylogenetic inferences from genome-wide snps. Systematic Biology, 63(2), 134–152.

Smith, J., & Kronforst, M. R. (2013). Do heliconius butterfly species exchange mimicry alleles? Biology Letters, 9(4), 20130503.

Zhang, W., Dasmahapatra, K. K., Mallet, J., Moreira, G. R., & Kronforst, M. R. (2016). Genome-wide introgression among distantly related heliconius butterfly species. Genome Biology, 17(1), 25.

Patterson, N., Price, A. L., & Reich, D. (2006). Population structure and eigenanalysis. PLoS Genetics, 2(12), e190.

Abraham, G., Qiu, Y., & Inouye, M. (2017). FlashPCA2: Principal component analysis of biobank-scale genotype datasets. Bioinformatics.

Duforet-Frebourg, N., Luu, K., Laval, G., Bazin, E., & Blum, M. G. (2015). Detecting genomic signatures of natural selection with principal component analysis: Application to the 1000 genomes data. Molecular Biology and Evolution, 33(4), 1082–1093.

Galinsky, K. J., Bhatia, G., Loh, P.-R., Georgiev, S., Mukherjee, S., Patterson, N. J., & Price, A. L. (2016). Fast principal-component analysis reveals convergent evolution of adh1b in europe and east asia. The American Journal of Human Genetics, 98(3), 456–472.

Luu, K., Bazin, E., & Blum, M. G. (2017). Pcadapt: An r package to perform genome scans for selection based on principal component analysis. Molecular Ecology Resources, 17(1), 67–77.

Messer, P. W., & Petrov, D. A. (2013). Population genomics of rapid adaptation by soft selective sweeps. Trends in Ecology & Evolution, 28(11), 659–669.

Hudson, R. R. (2002). Generating samples under a wright–Fisher neutral model of genetic variation. Bioinformatics, 18(2), 337–338.

Rambaut, A., & Grass, N. C. (1997). Seq-gen: An application for the monte carlo simulation of dna sequence evolution along phylogenetic trees. Bioinformatics, 13(3), 235–238.